6 Sampling Distribution of the Mean
The last two chapters has prepared us with foundation to start learning about statistical inference promised in Chapter 1. Recall that while descriptive statistics focuses on describing the sample data, inferential statistics tries to make conclusion about the population.
In this chapter, we will focus on the conclusion about the mean parameter in the population. Think about it: we usually want to ask questions like: What is the average height of Canadian men/women? How much does a Canadian earn on average? … In these cases, the mean of the population is exactly what we are interested in.
6.1 Sampling Distribution
6.1.1 Sample Random Variables
Consider a probabilistic experiment and \(n\) trials of that specific probabilistic experiment. Suppose we are interested in the random variable \(X\) of the probabilistic experiment. Since the outcome of each trial (run) is unknown unless we actually conduct the trials, the value of \(X\) for each trial is also unknown. Thus, they are also random variables, defined as follows.
\(X_1\): the value of \(X\) based on the outcome of the first trial
- Because I do not know the outcome of the first trial unless I conduct it, the value of \(X\) for the first trial is random. So, \(X_1\) is a random variable according to Chapter 4.
\(X_2\): the value of \(X\) based on the outcome of the second trial
- Similar to \(X_1\), \(X_2\) is also a random variable
…
\(X_n\): a variable based on the outcome of the \(n\)th trial
Now \(X_1, X_2, ...., X_n\) are random variables. Their values are random (unknown).
Example 6.1 Consider a familiar probabilistic experiment: tossing a coin and the variable \(X\) defined by \[X = \begin{cases} 1 & \text{if a head is obtained} \\ 0 & \text{if a tail is obtained} \end{cases}\]
If we toss \(n\) coins, i.e., if we have \(n\) trials of the coin tossing experiment, then
\(X_1\): whether a head is obtained in the first trial
\(X_2\): whether a head is obtained in the second trial
…
\(X_n\): whether a head is obtained in the \(n\)th trial
Example 6.2 Consider randomly selecting one student. I do not know who I will pick before I actually pick them. Hence, randomly picking one student is a probabilistic experiment. The student’s rent is the variable of interest and suppose we denote it as \(Y\). This is a random variable which is based on the student I pick, i.e., the outcome of my probabilistic experiment.
If I randomly select \(1000\) students. Then
\(Y_1\): rent of the first student.
\(Y_2\): rent of the second student.
…
\(Y_{1000}\): rent of the \(1000\)th student.
6.1.2 Independent Trials
\(n\) trials are said to be independent if the outcome of one trial does not affect the outcome of the another trial.
Example 6.3 Tossing a coin. Suppose the result of one coin toss, whether it is head or tail, does not affect the result of the next or next next or the next next … next coin toss. Then we says that the \(n\) coin tosses are independent trials.
Example 6.4 Suppose I pick the first random person on the street and ask about their rent (\(X_1\)). Then I let them suggest the next person to pick.
I do not know the second person I am going to pick before I pick the first person. So the next actual person I am going to pick is also random and the second person’s rent \(X_2\) is also a random variable.
However, the outcome of the second pick depends on the first pick. So \(X_2\) and \(X_1\) are not independent.
If our \(n\) trials are independent, then the random variables \(X_1, X_2, ...., X_n\) based on \(n\) independent trials are called independent.
6.1.3 Population Distribution
If the random variable \(X\) of the probabilistic experiment follows a probability distribution, then such probability distribution is called the population distribution.
Since \(X_1, X_2, ..., X_n\) are based on the results of \(n\) trials of the probabilistic experiments, they also follow the same distribution as \(X\). Notation: \[X_i \sim X, \hspace{10mm} i = 1, 2, ..., n\] We say that \(X_1, X_2, ..., X_n\) are identically distributed. Equivalently, we say \(X_1, X_2, ..., X_n\):
are drawn from distribution \(X\)
are sampled from distribution \(X\)
are identically distributed following \(X\)
follow distribution \(X\)
If in addition, \(X_1, ..., X_n\) are independent, we say that \(X_1, X_2, ..., X_n\) are independently and identically distributed (iid). Notation \[X_i \overset{\text{iid}}{\sim} X, \hspace{10mm} i = 1, 2, ..., n\]
Example 6.5 If \(X\) follows a \(\mathrm{Unif}(c, d)\) distribution, then we write \[X_i \sim \mathrm{Unif}(c, d), \hspace{10mm} i = 1, 2, ..., n\] and if \(X_1, ..., X_n\) are also independent, then we write \[X_i \overset{\text{iid}}{\sim} \mathrm{Unif}(c, d), \hspace{10mm} i = 1, 2, ..., n\]
6.1.4 Sampling Distribution
A statistic is a function of \(X_1, X_2, ..., X_n\). Being a function of random variables, the statistic itself is also a random variable.
The probabilistic distribution of a statistic is called the sampling distribution of the statistic. This means that if we repeat collecting different samples of fixed sample size \(n\) many times, and calculate the corresponding statistic from those different samples, we will obtain the sampling distribution of the statistic.
These definitions may seem very abstract. To understand these concepts thoroughly, it is best to put them into context. In that sense, let us discuss one of the most important example: the sample mean statistic.
6.2 Sample Mean
6.2.1 Sample Mean Random Variable
Suppose the random variable of interest \(X\) of the probabilistic experiment follows a distribution that has mean \(\mu\). That is, \(\mu\) is the population mean and hence a population parameter.
The sample mean/average of \(X_1, X_2, ..., X_n\) is \[\bar{X}_n = \frac{X_1 + X_2 + ... + X_n}{n} = \frac{1}{n}\sum_{i=1}^n X_i,\] which is a function of \(X_1, X_2, ..., X_n\). Therefore, it is a sample statistic.
Here, the notation \(\bar{X}_n\) stresses that the sample mean is calculated based on \(n\) trials. But sometimes we write \(\bar{X}\) instead of \(\bar{X}_n\) for simplicity. Because \(\bar{X}_n\) is calculated based on \(n\) random variables, it is itself also a random variable.
6.2.2 Observed Sample Means
Now, it is important to differentiate the sample mean random variable and the observed sample mean we learn from Chapter 2:
\(\bar{X}_n\): the random/unknown sample mean, i.e., the statistic, which is calculated from the trials’ random variables \(X_1, X_2, ..., X_n\)
\(\bar{x}_n\): the observed/realized sample mean, i.e., the observed statistic, which is calculated from the observed data
the observed sample mean \(\bar{x}_n\) (or for short, \(\bar{x}\)) is calculated from the observed values \(x_1, ..., x_n\) of the random variables \(X_1, ..., X_n\) when the \(n\) trials are conducted/realized.
I will write \(\bar{x}_n\) when I explain concepts and I will write \(\bar{x}\) for short when I solve example questions.
Example 6.6 Revisit Example 6.2. \(Y\): rent of the student picked. Suppose one day, I go and collect data from 5 randomly chosen students. The results are as follows:
| General unknown outcome of trial | General unknown value of \(Y\) | Known & realized outcome of trial | Known & realized value of \(Y\) |
|---|---|---|---|
| Person 1 | \(Y_1\): rent of person 1 | Tom | \(y_1 = 830\) |
| Person 2 | \(Y_2\): rent of person 2 | Mary | \(y_2 = 490\) |
| Person 3 | \(Y_3\): rent of person 3 | Steve | \(y_3 = 720\) |
| Person 4 | \(Y_4\): rent of person 4 | John | \(y_4 = 670\) |
| Person 5 | \(Y_5\): rent of person 5 | Sarah | \(y_5 = 1010\) |
Then \[\bar{Y}_5 = \frac{Y_1 + Y_2 + ... + Y_5}{5} = \text{the average rent of the 5 randomly selected people}\] and \[\bar{y}_5 = \frac{y_1 + y_2 + ... + y_5}{5} = \frac{830+490+720+670+1010}{5} = 744\] So here, \(\bar{Y}_5\) is a general and unknown quantity, a random variable. And \(\bar{y}_5 = 744\) is an actual number.
6.2.3 Sampling Distribution of the Sample Mean
If we repeat collecting random samples of the same sample size \(n\), each time we will obtain a different set of observed values \(x_1, x_2, ..., x_n\) and hence we will get a different value of \(\bar{x}_n\).
These different observed values of \(\bar{x}_n\) together form the distribution of the random variable \(\bar{X}_n\). This is called the sampling distribution of \(\bar{X}_n\).
Example 6.7 Revisit Example 6.1: tossing a coin and consider the random variable \(X\) which equals to \(1\) if a head is obtained, and equals to 0 if a tail is obtained.
Suppose that the coin is fair, then \[p_X(x) = \mathbb{P}(X = x) = \begin{cases} \frac{1}{2} & \text{if } x = 1 \\ \frac{1}{2} & \text{if } x = 0\end{cases}\] \(p_X(x)\) is the population distribution of \(X\).
Now, suppose I conduct 3 trials of the probabilistic experiment, i.e., I toss the coin 3 times.
\(X_1\): whether I obtain a head in trial 1
\(X_2\): whether I obtain a head in trial 2
\(X_3\): whether I obtain a head in trial 3
If I repeat tossing the coins 3 times for many times, each possible value of the trio \((X_1, X_2, X_3)\) has the same probability of happening. There are in total 8 possible combinations of \((X_1, X_2, X_3)\) so the probability of each to happen is \(1/8\). Therefore we have
| Probability of happening | Possible values of \(\{X_1, X_2, X_3\}\) | Value of \(\bar{X}_3\) |
|---|---|---|
| \(1/8\) | \(\{0,0,0\}\) | \(0\) |
| \(1/8\) | \(\{0,0,1\}\) | \(1/3\) |
| \(1/8\) | \(\{0,1,0\}\) | \(1/3\) |
| \(1/8\) | \(\{0,1,1\}\) | \(2/3\) |
| \(1/8\) | \(\{1,0,0\}\) | \(1/3\) |
| \(1/8\) | \(\{1,0,1\}\) | \(2/3\) |
| \(1/8\) | \(\{1,1,0\}\) | \(2/3\) |
| \(1/8\) | \(\{1,1,1\}\) | \(1\) |
Based on the table, the sampling distribution of \(\bar{X}_3\) is
\[p_{\bar{X}_3}(z) = \mathbb{P}(\bar{X}_3 = z) = \begin{cases} 1/8 & \text{if } z = 0 \\ 3/8 & \text{if } z = \frac{1}{3} \\ 3/8 & \text{if } z = \frac{2}{3} \\ 1/8 & \text{if } z = 1 \end{cases}\]
Note here that the sampling distribution of \(\bar{X}_3\) is different from the population distribution of \(X\).
Exercise 6.1 In Example 6.7, what is the sampling distribution of \(\bar{X}_4\)?
6.2.4 Expectation and Variance
6.2.4.1 Expectation and Variance of a Linear Combination of Random Variables
Generally, if \(X\) and \(Y\) are two random variables, then \[\mathbb{E}(aX + bY) = a\mathbb{E}(X) + b\mathbb{E}(Y) \] If further \(X\) and \(Y\) are independent, then \[\mathrm{var}(aX + bY) = a^2\mathrm{var}(X) + b^2\mathrm{var}(Y)\]
6.2.4.2 Expectation and Variance of the Sample Mean
Now, apply the above result to the sample mean. If \(X_1, X_2, ..., X_n \overset{\text{iid}}{\sim} X\) where \(\mathbb{E}(X) = \mu\) and \(\mathrm{var}(X) = \sigma^2\). Then \[\mathbb{E}(\bar{X}_n) = \mathbb{E}\left(\frac{X_1 + ... + X_n}{n}\right) = \frac{1}{n}\Big[\mathbb{E}(X_1) + ... + \mathbb{E}(X_n) \Big] = \frac{1}{n}n\mu = \mu\]
The variance is \[\mathrm{var}(\bar{X}_n) = \mathrm{var}\left(\frac{X_1 + ... + X_n}{n}\right) = \frac{1}{n^2}\Big[\mathrm{var}(X_1) + ... + \mathrm{var}(X_n) \Big] = \frac{1}{n}n\sigma^2 = \frac{\sigma^2}{n}\]
So the sample mean \(\bar{X}\) has mean \(\mu\) and variance \(\sigma^2/n\).
6.2.5 Sample Mean of Independent Normal Draws
Property (Linearity of normal distribution): A linear combination (i.e., \(a_1Y_1 + a_2Y_2 + ... + a_mY_m\)) of normally distributed random variables (\(Y_1, Y_2, ..., Y_m\)) is also a normal random variable.
Now, if we suppose further that \(X_1, X_2, ..., X_n\) are normally distributed. That is, \[X_i \overset{iid}{\sim} \mathcal{N}(\mu, \sigma^2), \hspace{5mm} i = 1, 2, ..., n\] then using the linearity property of normal distribution, we can deduce that the sample mean \(\bar{X}_n\) is also normally distributed with mean \(\mu\) and variance \(\frac{\sigma^2}{n}\). That is,
\[\text{If } X_1, X_2, ..., X_n \overset{\text{iid}}{\sim} \mathcal{N}(\mu, \sigma^2), \hspace{5mm} \bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_n \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\]
This means that the sample mean random variable \(\bar{X}_n\), i.e., the average calculated from \(n\) independent normal draws
is also normally distributed.
is unbiased for \(\mu\) because its bias is zero, in the sense that \[\mathbb{E}[\bar{X}_n] = \mu \hspace{5mm} \text{and} \hspace{5mm} \mathbb{E}[\bar{X}_n] - \mu = 0\] Let me explain this in words. Suppose I have \(m\) samples, for each sample I conduct \(n\) trials. For each sample I can calculate a value \(\bar{x}_n\) of \(\bar{X}_n\), say \(\bar{x}_n^{(1)}, \bar{x}_n^{(2)}, ..., \bar{x}_n^{(m)}\). Then, if \(m\) is large, the average of values \(\bar{x}_n^{(i)}\), \(i = 1, 2, ..., m\) will be the true parameter \(\mu\). We say that \(\bar{X}\) is unbiased of \(\mu\).
increases in precision as \(n\) increases: when \(n\) becomes larger, \(\mathrm{var}(\bar{X}_n)\) becomes smaller \[\lim_{n\to\infty}\mathrm{var}(\bar{X}_n) = \lim_{n\to\infty}\frac{\sigma^2}{n} = 0\] This means that
The spread of the distribution of \(\bar{X}_n\) becomes smaller. Hence, as \(n\) increases, realized values \(\bar{x}_n\) will tend to be closer to each other, and we say that \(\bar{X}_n\) becomes more precise (i.e., its variance decreases) as \(n\) increases (Recall the definition of precision in Chapter 1).
Smaller variance \(\mathrm{var}(\bar{X}_n)\) also means that the distribution of \(\bar{X}_n\) pulls more towards the center as \(n\) increases, i.e., the distribution becomes closer to the mean \(\mathbb{E}(\bar{X}_n)\). But \(\mathbb{E}(\bar{X}_n) = \mu\). In this sense, the sample mean \(\bar{X}_n\) will get closer to the population mean \(\mu\) as our population becomes bigger.
This is logical because if our sample size is large, our sample will contain more units from the population. Thus our sample will get closer to population.
We say that \(\bar{X}_n\) estimates the population mean \(\mu\) better when \(n\) is large.
This is the reason why we want large sample size \(n\) in Chapter 1.
The figure below shows the distribution of \(\bar{X}_n\) for \(n = 1, 2, 4\) if \(X \sim \mathcal{N}(0, 10)\).
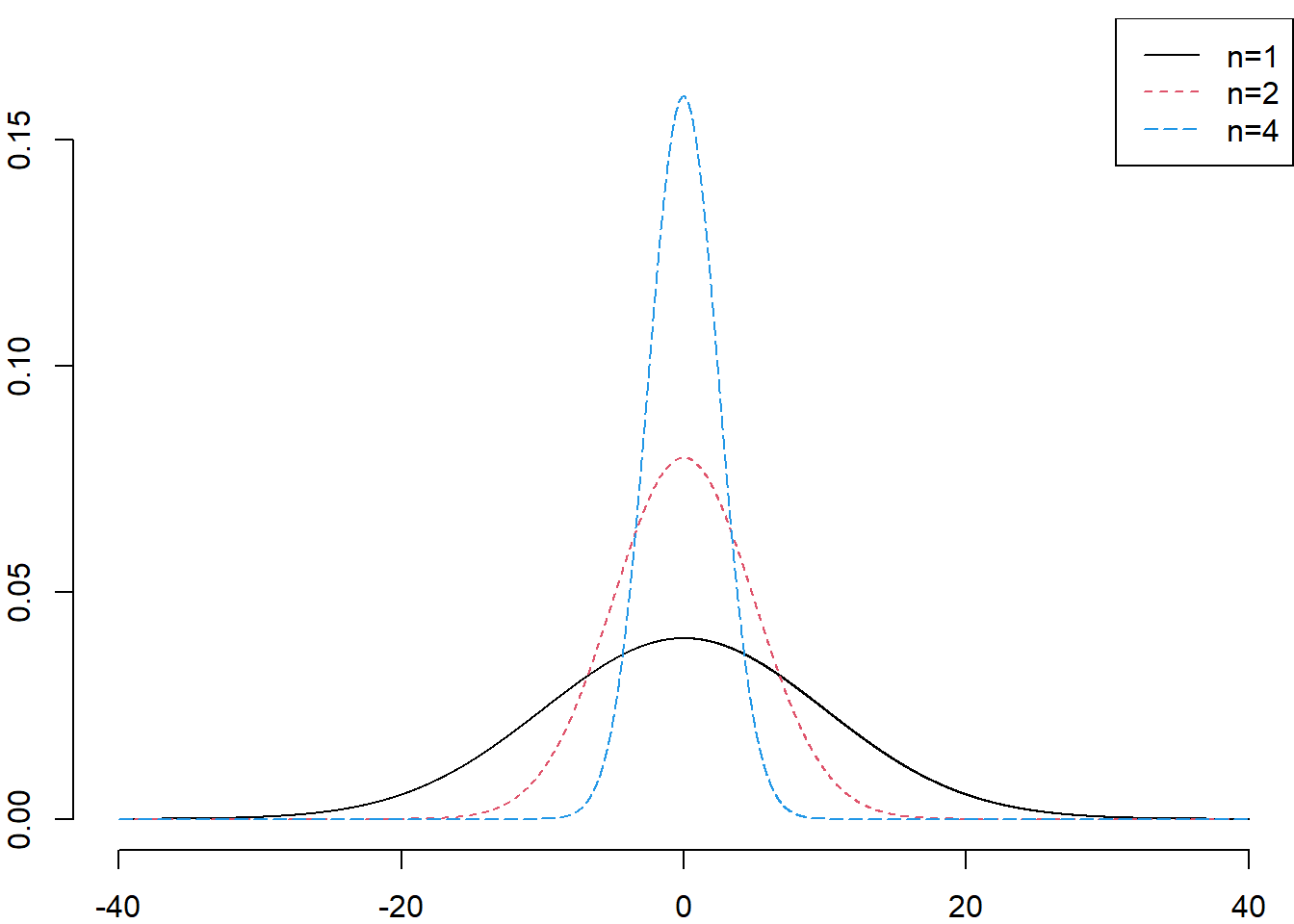
Figure 6.1: The sampling distribution of \(\bar{X}_n\) if we are sampling from a \(\mathcal{N}(0, 10)\) population.
Example 6.8 Suppose that 16 observations are randomly selected from a normally distributed population where \(\mu = 10\) and \(\sigma^2 = 625\).
What is the distribution of \(\bar{X}\)?
What is \(\mathbb{P}(\bar{X} > 30)\)?
What is \(\mathbb{P}(0 < \bar{X} < 20)\)?
Solution:
Because \(\bar{X}_n \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\). Hence, for this problem17 \[\bar{X} \sim \mathcal{N}\left(10, \frac{625}{16}\right)\]
Because \(\bar{X}\) is normally distributed, we use the standard normal distribution to solve for probability of \(\bar{X}\). \[\begin{align*} \mathbb{P}(\bar{X} > 30) & = \mathbb{P}\left(Z > \frac{30-10}{\sqrt{\frac{625}{16}}}\right) \\ & = \mathbb{P}(Z > 3.2) \\ & = \mathbb{P}(Z < -3.2) \\ & = 0.0007 \end{align*}\]
\[\begin{align*} \mathbb{P}(0 < \bar{X} < 20) & = \mathbb{P}\left(\frac{0-10}{\sqrt{\frac{625}{16}}} < Z < \frac{20-10}{\sqrt{\frac{625}{16}}}\right) \\ & = \mathbb{P}(-1.6 < Z < 1.6) \\ & = \mathbb{P}(Z < 1.6) - \mathbb{P}(Z < -1.6) \\ & = \mathbb{P}(Z > -1.6) - \mathbb{P}(Z < -1.6) \\ & = 1 - \mathbb{P}(Z < -1.6) - \mathbb{P}(Z < -1.6) \\ & = 1 - 2\times \mathbb{P}(Z < -1.6) \\ & = 1 - 2 \times 0.0548 = 0.8904 \end{align*}\]
Example 6.9 Assume that the the price of games sold on iPad is normally distributed with a mean of \(\$3.48\) and a standard deviation of \(\$2.23\).
What is the probability that the price of one randomly selected game lies between \(\$3.50\) and \(\$4.00\)?
If 40 games are randomly selected, what is the probability that the average price of these games lies between \(\$3.50\) and \(\$4.00\)?
Solution: Let \(X\): price of a randomly selected iPad game. Then \(X \sim \mathcal{N}(3.48, 2.23^2)\).
\[\begin{align*} \mathbb{P}(3.5 < X < 4) & = \mathbb{P}\left(\frac{3.5-3.48}{2.23} < Z < \frac{4-3.48}{2.23} \right) \\ & = \mathbb{P}(0.01 < Z < 0.23) \\ & = \mathbb{P}(Z < 0.23) - \mathbb{P}(Z < 0.01) \\ & = \mathbb{P}(z > -0.23) - \mathbb{P}(z > -0.01) \\ & = (1 - \mathbb{P}(Z < -0.23)) - (1 - \mathbb{P}(Z < -0.01)) \\ & = \mathbb{P}(Z < -0.01) - \mathbb{P}(Z < -0.23) \\ & = 0.4960 - 0.4090 = 0.0870 \end{align*}\]
Because there are 40 samples, \(\bar{X} \sim \mathcal{N}\left(3.48, \frac{2.23^2}{40}\right)\). So \[\begin{align*} \mathbb{P}(3.5 < \bar{X} < 4) & = \mathbb{P}\left(\frac{3.5-3.48}{\frac{2.23}{\sqrt{40}}} < Z < \frac{4-3.48}{\frac{2.23}{\sqrt{40}}}\right) \\ & = \mathbb{P}(0.06 < Z < 1.47) \\ & = \mathbb{P}(Z < 1.47) - \mathbb{P}(Z < 0.06) \\ & = (1-\mathbb{P}(Z < -1.47)) - (1-\mathbb{P}(Z < -0.06)) \\ & = \mathbb{P}(Z < -0.06) - \mathbb{P}(Z < -1.47) \\ & = 0.4761 - 0.0708 = 0.4053 \end{align*}\]
6.2.6 Central Limit Theorem
Suppose \(X_1, X_2, ..., X_n\) are independent and identically distributed random variables from a population with mean \(\mu\) and standard deviation \(\sigma\). That is \[X_1, X_2, ..., X_n \overset{\text{iid}}{\sim} (\mu, \sigma^2)\] where \(\sigma^2 < \infty\).
Then the Central Limit Theorem states that when \(n\) is large the sample mean \(\bar{X}_n\) is approximately normally distributed with mean \(\mu\) and variance \(\frac{\sigma^2}{n}\). That is,
\[\text{If } X_1, X_2, ..., X_n \overset{\text{iid}}{\sim} (\mu, \sigma^2), \text{ when $n$ is large:} \hspace{5mm} \bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_n \overset{\cdot}{\sim} \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\]
where \(\overset{\cdot}{\sim}\) means approximately follows.
Notes:
Regardless of the population distribution that we are sampling from, if the sample size \(n\) is large, the sample mean \(\bar{X}_n\) will always be approximately normal.
Under most conditions, sample size \(\mathbf{n > 30}\) will be sufficient for good approximation.
The Central Limit Theorem shows us once again the importance of normal distribution in Statistics.
Example 6.10 Suppose that house prices in a very large city are known to have a mean of \(\$389,000\) and a standard deviation of \(\$120,000\). What is the probability that the mean price of \(100\) randomly selected houses is more than \(\$400,000\)?
Solution:
Let \(X\): price of a randomly selected house in the city.
We do not now the distribution of \(X\), only its mean and standard deviation.
We are interested in the mean price.
The sample size \(100\) is greater than 30.
For the above reasons, we can use the Central Limit Theorem and have
\[\bar{X} \sim \mathcal{N}\left(389000, \frac{120000^2}{100}\right)\]
Now we can solve for the probability asked in the question
\[\begin{align*} \mathbb{P}(\bar{X} > 400000) & = \mathbb{P}\left(Z > \frac{400000 - 389000}{120000/\sqrt{100}}\right) \\ & = \mathbb{P}(Z > 0.92) \\ & = \mathbb{P}(Z < -0.92) = 0.1788. \end{align*}\]
Example 6.11 A manufacturer of automobile batteries claims that the distribution of the length of life of its batteries has a mean of \(54\) months and a standard deviation of \(6\) months. Recently, the manufacturer has received a rash of complaints from unsatisfied customers whose batteries have died earlier than expected. Suppose a consumer group decides to check the manufacturer’s claim by purchasing a sample of \(50\) of these batteries and subjecting them to tests that determine battery life.
Assuming that the manufacturer’s claim is true, what is the probability that the consumer group’s sample has
A mean life of \(52\) or fewer months?
A mean life between 52 and 56 months?
Solution:
Let \(X\): life times of randomly selected battery.
We again do not know the distribution of \(X\), only its mean and standard deviation. We are interested in the sample mean of \(50 > 30\) randomly selected batteries. So we can use the central limit theorem:
\[\bar{X} \sim \mathcal{N}\left(54, \frac{6^2}{50}\right)\]
\[\mathbb{P}(\bar{X} \le 52) = \mathbb{P}\left( Z \le \frac{52 - 54}{\frac{6}{\sqrt{50}}} \right) = \mathbb{P}(Z \le -2.36) = 0.0091\]
\[\begin{align*} \mathbb{P}(52 \le \bar{X} \le 56) & = \mathbb{P}\left(\frac{52-54}{\frac{6}{\sqrt{50}}} \le Z \le \frac{56-54}{\frac{6}{\sqrt{50}}}\right) \\ & = \mathbb{P}(-2.36 \le Z \le 2.36) \\ & = \mathbb{P}(Z \le 2.36) - \mathbb{P}(Z \le -2.36) \\ & = 1 - 2\times \mathbb{P}(Z \le -2.36) \\ & = 1 - 2\times 0.0091 = 0.9818. \end{align*}\]
Notes: This chapter started by introducing concepts that are very abstract, especially when I talk about sampling distribution. My intention is to give you some feeling about the abstract concepts. And at the same time I do not want to make you misunderstand the concepts by explaining something too casually. However, I have included a lot of examples to help illustrate what I say. You can go back and forth between the explanation and the examples to try to understand things more clearly.
We write \(\bar{X}\) instead of \(\bar{X}_n\) for simplicity.↩︎