1 Four Research Steps
1.1 Why Statistics?
Curiosity, as a part of human nature, motivates us to ask questions and find answers. Imagine our ancestors in their early days. Every night, around the fire, they might have looked at the sky and observed the shapes of the moon changing from day to day, and asked themselves if there is any principle to such changes. They might have started by counting the days between two full moons and found a roughly 30-day difference. Will this be true all the time, or is it true only for this instance? To answer this, they might have had to continue to count the days from month to month, year to year, to finally understand the moon cycle.
This answer-finding process can be applied to almost any question in our lives. Starting with a question or a general area of interest, we collect data (information) around the topic, look at the data to find pattern, and form an answer to the question. We can stop there if we are satisfied with the answer, or we can modify the question, continue to collect data, revise the answer, and so on. These are the main steps of a general research process, which can be summarized in Figure 1.1.

Figure 1.1: General research process
Statistics is the study of data1, hence it involves all steps of the general research process. In particular, statistics will help us with
- forming our research questions in a way that it can be answered using data,
- designing the data collecting process,
- extracting information from the data collected, and
- making an informed (data-driven) conclusion.
Therefore, we can think of statistics as a supporting field for almost all data-related or quantitative sciences. Besides general procedures and techniques, specialized statistical methods can be developed to cater to specific research areas with specific types of data and requirements. Some specializations of statistics are biostatistics, econometrics, psychometrics, etc. In fact, many important methods in statistics were developed by non-statisticians. This emphasizes the interdisciplinary nature of statistics and its important role in scientific research. Knowing statistics will help you understand and critically evaluate published research and conduct research yourselves. Therefore
LET’S LEARN STATISTICS!
In this chapter, we will briefly describe each step in Figure 1.1 while learning some important definitions and concepts in statistics.
1.2 Research Question
Let’s start with the first step of a research: forming a research question. What can be a research question? And how to look at this research question in a statistical way?
1.2.1 Variables
A variable is a characteristic or quantity which can take different values. A variable can be
qualitative: characteristics that can be described or categorized into categories.
Some examples are
gender: this can take the values of female, male, or others;
education: this can take the values of high school, undergraduate, graduate, etc.
quantitative: characteristics that can be described or quantified by numerical values.
Some examples are
height: this can take numerical values such as 165cm, 180cm, 155cm, etc.
age: this can take numerical values such as 19, 5, 67, etc.
Variables form the topics of research goals:
We may want to understand one variable.
- e.g., What are the ages of people when they enter college? How much do Canadians earn this year? etc.
We may want to understand the relationship among multiple variables.
- e.g., the relationship of gender and income, of age and height, of location and house price, etc.
We may want to predict the value of one variable given the values of some other variables
- e.g., predict the final exam score given the midterm exam score; predict income given gender, years of education, job types, etc.
If a research is involved with more than one variable, there is usually only one variable of main interest. This is the variable whose trends you want to understand or the one which you want to make predictions about. This variable is called the response variable (also known as the dependent variable). Other variables that help explain or predict the response variable are called the explanatory variables (also known as the independent variables).
Notes: I think it is now a good time to take an example. I will use this example throughout the book to explain statistical concepts. This is because I myself find it an easier way to understand, especially, a chapter packed with new concepts like this one. For those of you who are new to statistics, the amount of new terminology in this lesson may seem intimidating. I strongly recommend you to think of another example of your own, and then apply or explain the new definitions in the context of your example. Having your own examples and trying to explain them yourself will be extremely useful to help you clearly understand new ideas and definitions.
Example 1.1 Suppose I am interested in how much students pay for rent. Then rent is my response variable. If furthermore I also want to know if gender or level of study (undergraduate/graduate) affects how much students pay for rent. Then gender and level of study will be my explanatory variables.
Exercise 1.1 If I am interested in people’s income, what is my response variable, and what can be my explanatory variables?
1.2.2 Inference and Prediction
In general, there are two general goals of statistics:
inference: understanding and inferring a principle of the current situation, and
prediction: making an informed guess about an unseen situation or the future.
Different statistical techniques are developed for each of the two goals. Classical statistics usually involves inference, while the recently popular machine learning researches focuses on prediction.
Example 1.2 Continue with the rent example. Now, if I am interested in knowing if female students pay more for rent compared to male students, my goal will be inference.
On the other hand, if, for example, I meet a new friend and I know that he is an undergraduate student, based on the data I collected about other students, I want to guess how much he is paying for rent. Now my goal would be prediction.
1.2.3 Population and Sample
Units (or individuals, or cases) are the objects on which the values of the variables are measured or recorded. In the student rent example, “students” will be our study units.
Example 1.3 Now that I know the topics of my research (i.e., the variables), I will need to decide the scope of my research. Who do I want to make conclusions about? Do I want to understand the monthly rent expense of UWaterloo students, or do I want to know the monthly rent expense of all Canadian students?
Population is the entire group of units that we want to make conclusions about.
Example 1.4 Suppose I want to understand the monthly rent expense of UWaterloo students. If I want to understand this exactly, I will need to ask every single student studying at University of Waterloo how much they are paying for rent. But will that ever be possible? There are tens of thousands of students studying at UWaterloo.
So instead, I will try to get a sense of the monthly rent expense of UWaterloo students by walking around the campus and asking them how much they are paying for rent. However, I cannot meet every student, and even if I’m committed to see every UWaterloo student, it will take a tremendous amount of time to do so. In the end, I will only be able to collect the rent data from some students. This is called the sample for my study.
A sample is the specific group of units on which we collect our data.
Example 1.5 Because I will walk around the campus to ask students about their rent, I will only be able to collect information from ones who actually walk on campus, and I will hardly meet anyone who studies remotely. Furthermore, a person who walks on campus needs not to be a student. In this case, the group that I am able to survey is different from the group that I want to research.
Because of the way we collect our data, there will be two types of population:
Target population: the group of units that you want to make conclusions about.
Accessible population (or study population): the group of units that you are actually able to get access to.
When these two types of population coincide, we just call both of them population for short.
In summary, we want to use data of the sample to make conclusions about the target population. However, due to the way we collect our data, we are only able to collect data from the accessible population, and hence our conclusions will be most valid on the accessible population.
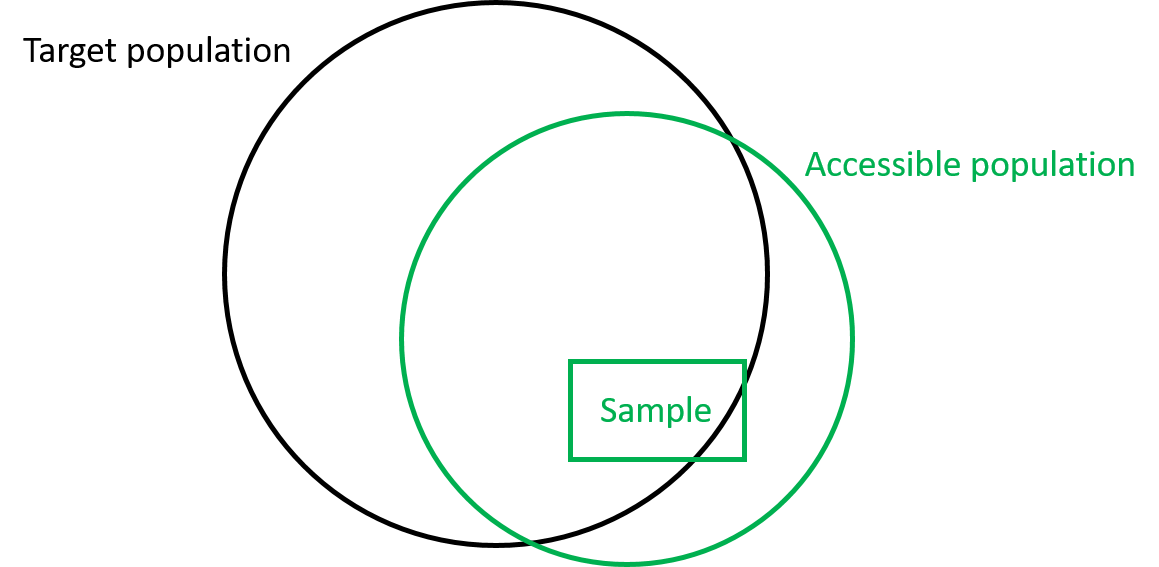
Figure 1.2: Population and sample
Example 1.6 Describe a situation when the accessible population and the target population are the same, and when they are not the same.
Exercise 1.2 Cannabis has recently been legalized in Canada. We want to understand the use of cannabis by adult Canadians by surveying 1000 Canadians by phone.
What can be the variables that we want to collect information about?
What is the target population?
What is the accessible population? Is it the same with the target population? Is it a subset of the target population?
Describe the sample obtained.
1.2.4 Parameter and Statistic
Example 1.7 Now we collect the data about students’ rent, there will be tens to hundreds of observations in our sample. We can look at each observation on its own, for example, how much Phillip, or Sophia, or Jeremy pays for their rent this month. In this way, we will know more about Phillip, and Sophia, and Jeremy. But what can we say about the rent paid by UWaterloo students in general? How can we understand the tens or hundreds of individual observations in a collective way? The answer is, we need to summarize the data.
A parameter is a quantity that can be calculated from the population. A statistic is a quantity that can be calculated from the sample. For each parameter, there will be a corresponding statistic.
Example 1.8 Continue with our rent example, we may be interested in how much UWaterloo students are paying for rent on average. The parameter here is the population average. The corresponding statistic is the average rent that we calculate from the data in our sample.
Exercise 1.3 Suppose now I am interested in the vaccination rate in Canada. What is my parameter of interest and what is its corresponding statistic?
We can calculate the value of a statistic from the collected sample, thus we know the value of the statistic. However, we cannot calculate or know the value of the parameter because we cannot collect all information in the population. Hence, the value of a population parameter is often unknown2.
So, the goal of statistics is to use a sample statistic3 to make conclusions about a population parameter.
1.3 Data Collection
1.3.1 Variability and Bias
1.3.1.1 Fixed Population and Random Sample
Example 1.9 In the rent example, our population is the whole group of students studying at University of Waterloo. In a semester, this set will likely be unchanged. However, in the next semester, there may be students who graduate and new students who just begin. In this case, the population may be different from one semester to another.
However, in basic statistics, we usually assume that our population is fixed and the population parameter of interest is thus a fixed quantity4.
While the population is assumed fixed, the sample israndom.
Example 1.10 To understand the average rent expense of UWaterloo students, I decide to walk around the campus and ask 100 students about their rent expenses. In this case, my sample will contain 100 observations (i.e., my sample size is 100).
However, the list of these 100 people are not pre-determined. If I were to go on another day, there will be a high chance that the people I will meet will be different from the people I am going to meet today. That is, today, I will meet these 100 people just by chance. I do not know who I am going to meet before I actually meet them. In this case, I have a random sample.
If I repeat the data collection process on several days, I will receive a different sample and thus a different statistic every time I conduct the data collection.
1.3.1.2 Variability
The difference among the different observed samples of the same sampling method is called the variability of the sampling method. A sampling method with low variability is a sampling method with high precision.
Example 1.11 Suppose I randomly choose one region in Waterloo and Kitchener and then ask students in that region about their rent. In this case, my sampling scheme will have a high variability or a low precision.
This is because if I repeat this same sample collecting method for many times, every time I will interview students living in a different region. Since rent will depend on specific regions and their distances to school, the rent data I collect will tend to be substantially different from one sample to another.
1.3.1.3 Bias
The difference between the population and the average of different samples (coming from the same sampling method) is called the bias of the sampling method. Small bias means high accuracy.
Example 1.12 Suppose I only interview female students. Even if I repeat this same sample collection method many times, I only get the data that tells me about the rent price for female students. This data will likely be different from the rent price of all students on campus. Hence I say the bias is high and accuracy is low.
Figure 1.3 summarizes concepts about bias, variance, accuracy and precision.

Figure 1.3: Accuracy and precision.
1.3.2 What Makes A Good Sample?
Because we want to use the sample to understand the population, we need the sample to produce an accurate and precise estimate of the population parameter. To increase accuracy and precision, i.e., to decrease variability and bias, we want our sample to be
large because the more units we observe, the closer we will be to the population. Our sample will then be more accurate. It will also be more precise because when the sample is large, the possible samples will be not very different from each other.
representative of the population. This way, the sample will resemble the population and our estimator will be more accurate.
With a good sample, we can generalize our results to the population with better confidence.
1.3.2.1 Unmeasured Variables
There can be infinitely many possible variables that influence or interact with the response variable that we are interested in. And we can never be able to collect information about all those variables. The variables that can affect the variable of interest, but are not recorded in the data are called unmeasured variables.
Example 1.13 Together with gender and level of study, personal lodging preference can be a factor that affects the rent price that a student is paying. However, it is hard to measure this variable, hence it is one of the unmeasured variables.
1.3.2.2 Representative Sample
A representative sample needs to be representative of all variables, even unmeasured ones.
If a sample is not representative of a variable, there will be a systematic difference between the sample and the population, which will introduce bias on our estimator. In this case, we call this a biased sample. (Refer to Example 1.12)
If the accessible population is not representative of the target population, we have a study bias.
If the sample is not representative of the accessible population, we have a sample bias.
Exercise 1.4 Suppose I am interested in Canadians’ overall happiness. I am going to call them by phone to ask them questions about happiness. In what way can my sample be biased, and which bias is it?
1.3.3 Sampling Schemes
There are many sampling methods (a.k.a sampling schemes or protocols) that can be used to select a sample. These can be divided into two categories: non-probabilistic and probabilistic sampling schemes.
1.3.3.1 Non-Probabilistic Sampling Schemes
Non-probabilistic sampling schemes are ones where the samples are not chosen randomly. These include
Convenience sample: units that are convenient for us to collect data from.
Self-selection: units who volunteer to be a part of the sample.
Judgment sampling: units are selected based on our judgment.
Quota sampling: first divide the population into mutually exclusive subsets, then in each subset, select some units based on judgment.
Since with non-probabilistic sampling, the samples are not chosen randomly, they become more deterministic. This means that the variability of the statistics calculated from these samples will be low, i.e., the different possible samples will not be very different from each other.
However, because of the non-randomness, there are potentially unmeasured variables where our judgment cannot cover, thus the sample may not be representative of the population. In this sense, the bias will be high.
Example 1.14 Continue with our rent example. A convenience sampling scheme will be to ask our friends about their monthly rent. A self-selection scheme would be to hold a billboard on campus to ask for volunteers. A judgment sampling scheme would be to select people based on our intuition or judgment.
The samples obtained by these sampling schemes will likely be biased. This is because we are only asking people that we like or people who tend to volunteer. These people may have the same preference about housing and because of that, our sample will not be representative of the population and is thus biased.
1.3.3.2 Probabilistic Sampling Schemes
Probabilistic sampling schemes select samples in a random way. The randomness will eliminate the effect of any unmeasured variables, making the sample more representative and the bias will be reduced. Common schemes include
Simple random sampling (SRS): List all the units in the population, then randomly choose a fixed number of units in the list.
In this scheme, each unit has the same chance of being selected.
However, it is hard to conduct this sampling scheme because we are usually not able to get a full list of all the units in our population.
Stratified random sampling: Divide the population into mutually exclusive subgroups called strata. Then we apply an SRS on each stratum.
Stratified sampling helps us increase the representativeness level of our sample.
At the same time, it will decrease the variability because we are randomly selecting units from smaller sub-populations.
Cluster sampling: The units in the population are grouped into clusters. These clusters are usually pre-defined, such as provinces, cities, classes, etc. We then do an SRS on the clusters to select several specific clusters. After that, we include all the units in the chosen clusters in our sample.
Because the clusters are usually pre-defined, cluster sampling induce less administrative cost.
Depending on the characteristics of the population and the clusters, cluster sampling can increase or decrease the variability.

Figure 1.4: Stratified and cluster sampling
Example 1.15 If I were to use stratified sampling, I will divide UWaterloo students according to each faculty. In each faculty, I will randomly choose students to be included in my sample. However, it can be hard to get a full list of the students in each of the faculty.
If I were to use cluster sampling, I will randomly select a number of courses from UWaterloo’s course list. I will then go to ask all the students in those chosen courses about their monthly rent.
Exercise 1.5 In which situations will cluster sampling will decrease or increase variability?
We can also combine different sampling schemes by applying each scheme at a different stage. This is called multiple-stage sampling.
Example 1.16 In our rent example, a multi-stage sampling scheme I can use is that I will divide the population into faculties, and in each faculty, I sample among the courses given by that faculty. Then I will interview all students taking those selected courses.
Exercise 1.6 If my population of interest is Canadian citizens, describe a sampling scheme that you will recommend to me and explain why it will result in a representative sample.
1.3.4 Observational and Experimental Studies
Having chosen the sample, we need to think about how we are going to collect the data from the sample. At this stage, we can choose to conduct an observational study or an experimental study.
Observational study: is when we collect pre-existing information.
- In an observational study, we can only observe the existing situation, and thus we can only conclude about the association among the variables5.
Experimental study: is when we manipulate (or control) some explanatory variables and then collect the information about the response variables.
- In an experiment, we can observe the change in the response variables when the explanatory variable is intentionally changed. With data collected from the experiment, we may conclude about the causal relationship between the explanatory and the response variables.
Example 1.17 Coming back to the rent example. If I choose to ask students about the rent they are currently paying, I am conducting an observational study. I can also collect information about, say, the price of their winter coat. I may find that the higher the price of their winter coat, the higher the monthly rent they pay. I can say that rent expense and winter coat price are associated with each other. But I cannot conclude that high winter coat price causes high rent expense.
If instead I choose to conduct an experimental study in this way: I give some students in my sample cheaper winter coats, and some other students more expensive winter coats. After that, I let them choose a place to rent among a list of places with different prices. Now, if I find that the students who are given expensive coats choose more expensive places to rent, I may be able to conclude that high winter coat price causes high rent expense because students’ rent choice was made given the price of the winter coat.
Experiments can be very useful compared to observational studies because it can support causal conclusions. Indeed, if we can find the cause of something, we can change/manipulate the cause to obtain the desired result.
However, in many situations, experiments are not possible at all due to time, money, or ethical reasons. For example, if I want to know if smoking causes lung cancer, I cannot force any person to smoke! In those cases, observational study will be our only choice.
Example 1.18 In Example 1.17, suppose I choose to conduct the experiment I described. In what situation will my conclusion about the causal relationship between winter coat price and rent expense go wrong?
1.3.4.1 Confounding Variables
In an observational study, because we only observe the current, existing situation, we will only be able to make conclusions about the association among the variables. The best effort that we can make in an observational study is to try to obtain a sample that is as representative as possible so that our conclusion about the association is accurate and generalizable to the population.
On the contrary, even in an experiment, a causal conclusion (A causes B) can still be difficult to make due to confounders.
A confounder (a.k.a confounding or lurking variable) is a variable that influences both the response variable and the explanatory variable. Because of the confounder, we cannot separate the effect of the explanatory variable from the effect of the confounder on the response variable. In other words, we cannot conclude whether the change in the response variable is due to the explanatory variable or due to the confounder.
Example 1.19 Winter coat price and rent expense may both be influenced by budget. People with higher budgets may tend to buy more expensive winter coats and rent more expensive places. So even with the experiment described in the Example 1.17, we cannot conclude whether the higher rent we observe is due to a more expensive winter coat or because of a higher budget. This can be illustrated in Figure 1.5.
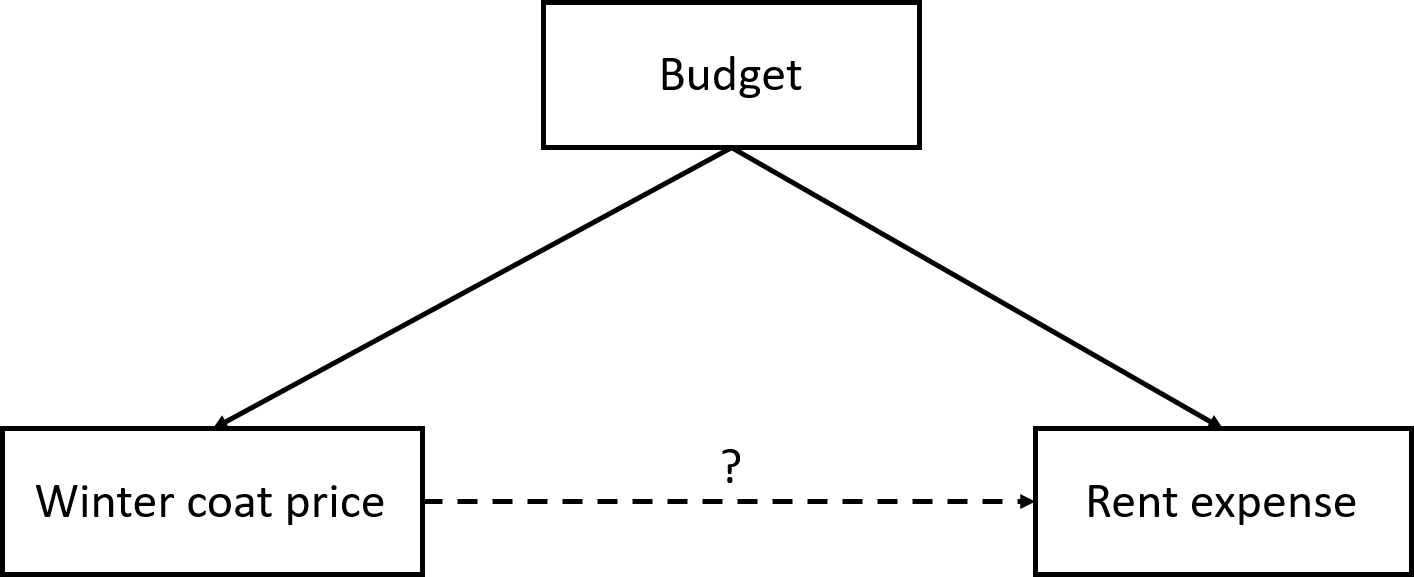
Figure 1.5: Relationships of winter coat price, budget and rent expense.
1.3.4.2 Neutralizing Confounders
To neutralize the effect of a confounder, we can
control the confounder at specific levels, and/or
randomly assign the experimental conditions to sample units.
In practice, to neutralize the effects of all possible confounders, scientists try to randomly assign the experimental conditions to sample units. These are called random controlled trials (RCTs). With RCTs, causal conclusions can be made with better confidence.
Example 1.20 To eliminate the effect of budget, I can give all students in my samples the same budget. Then I proceed to give some of them expensive coats and some of them cheaper coats and let them choose among different places of different prices. If the group who receive expensive coats still choose places with higher rent, I am more confident to say that winter coat price causes rent expense. However, be aware that this causal relationship is only happening on the level of budget that I give them. We are still not sure if I give them more or less budget, the relationship still exists or not.
I can also try to randomly divide my samples into two groups, one group will be given expensive coats and one group will be given cheaper coats. Because of the randomization, each group will hopefully have the same variety of budgets, and the association between winter coats and budget is removed. Now we can make a causal conclusion.
Exercise 1.7 Researchers are interested in investigating whether smoking causes lung cancer.
- Identify the response variable of interest.
- Identify the explanatory variable of interest.
- Describe a possible confounding variable.
1.4 Data Analysis
Having collected the data we need, we can proceed to analyze the data. In doing so, we can provide both descriptive and inferential statistics.
Descriptive statistics helps us describe, show or summarize our data set in a meaningful way.
Some examples of descriptive statistical techniques are visual plots or summary statistics (for example, average of rent in our sample).
With descriptive statistics, we can get a better sense of the data. We can also notice some patterns in our data. However, these impressions are only valid for our sample.
Inferential statistics helps us make generalizations or conclusions about the population. In other words, it helps us move from the sample to the population.
- Because we do not have data about the whole population, the conclusions will be made with uncertainty. Inferential statistics attempts to give us a sense of the level of uncertainty associated with our conclusion.
In the next chapter, we will cover some topics in descriptive statistics. The rest of the course will be dedicated to inferential statistics.
The term statistics usually does not include the study of data input, storage, retrieval, or data management in general. These topics are covered in data engineering.↩︎
Sometimes you can know some of the population parameter. Think about the Canadian Census.↩︎
This is not always the corresponding statistic. Sometimes we will modify them a bit to better estimate the population parameter.↩︎
This is a frequentist point of view. Bayesian statistics assumes that the population parameters are random. Nevertheless, in this course, we will only focus on frequentist statistics, which is the most popular in practice.↩︎
Association does not imply causation. You can see some examples of spurious associations (two variables that are related to each other but they do not cause one another) here.↩︎