10 Other Useful tests
In Chapter 8 and 9, we have been introduced to Wald-type tests, which are fundamental methods in statistics. However, there are other statistical hypothesis tests that will be useful to answer different questions for different situations. In this lesson, we will learn some of those tests. In doing so, we will only focus on the (i) hypotheses of the test; (ii) assumptions made for each test and (iii) the analysis procedure in R.
10.1 ANOVA
In Lesson 8 and 9, we learned about tests that (i) compare the mean of one population to a specific number (one-sample \(t\)-test) (ii) compare the means of two populations (two-sample \(t\)-test). What if we have more than two populations?
Example 10.1 Let’s come back to the student’s rent case. We want to know if the rent expense of students from all faculties are the same.
Now, suppose I have \(m\) populations \(X^{(1)}, X^{(2)}, ..., X^{(m)}\) and we want to test whether the means of these population are equal. A useful statistical tool to do so this is the (one-way) ANOVA (analysis of variance).
10.1.1 Assumptions
The \(m\) populations are independent
For each population \(i\) in the \(m\) populations, \(X^{(i)} \sim N(\mu_i, \sigma^2)\) and we have \(n_i\) observations \(X^{(i)}_1, X^{(i)}_2, ..., X^{(i)}_{n_i}\). This means
each population all follow normal distributions
the normal distributions may have different populations means \(\mu_1, \mu_2, ..., \mu_m\)
the normal distributions must have same variance \(\sigma^2\)
Example 10.2 Continue with Example 10.1, the ANOVA procedure assumes that the rent expense
For Arts: \(X^{(1)} \sim N(\mu_1, \sigma^2)\)
For Engineering: \(X^{(2)} \sim N(\mu_2, \sigma^2)\)
For Environment: \(X^{(3)} \sim N(\mu_3, \sigma^2)\)
For Health: \(X^{(4)} \sim N(\mu_4, \sigma^2)\)
For Math: \(X^{(5)} \sim N(\mu_5, \sigma^2)\)
For Science: \(X^{(6)} \sim N(\mu_6, \sigma^2)\)
We also assume that the rent expense of students coming from one faculty does not affect the rent expense of students coming from another faculty (independence)
In our data, we have \(n_1\) students coming from Arts, \(n_2\) students coming from Engineering, \(n_3\) students coming from Environment, \(n_4\) students coming from Health, \(n_5\) students coming from Math and \(n_6\) students coming from Science.
Notes: In ANOVA, it is preferred, but not required, that the sample sizes are equal for each population, i.e., \(n_1 = n_2 = ... = n_m\).
10.1.2 Hypotheses
ANOVA wants to test the following two hypotheses
\(H_0:\) \(\mu_1 = \mu_2 = ... = \mu_m = \mu\)
\(H_1:\) at least one of \(\mu_i\) differs from the rest of the population means.
Example 10.3 In Example 10.2, we want to test if the mean rent expenses of students coming from the six faculties equal.
10.1.3 Analysis in R
To conduct an ANOVA in R, we use function aov().
Example 10.4 To know if the mean rent are different among the different faculty values, we conduct an ANOVA on the data set we have collected fakeRent.csv. We use the following R code
#do an anova of variable rent with respect to variable faculty
#the two variables are called rent and faculty of the data set called `rent`
#memorize the anova results into an object called rentFaculty
rentFaculty <- aov(rent~faculty, data = rent)
#show the summary of the anova results
summary(rentFaculty)## Df Sum Sq Mean Sq F value Pr(>F)
## faculty 5 144104 28821 1.516 0.182
## Residuals 1339 25453319 19009There are many information in this summary, however, for the sake of conciseness for this book, we just focus our attention to the \(p\)-value (Pr(>F)). The \(p\)-value is \(0.182\), which is greater than our usual level of significance level \(0.05\), so we do not reject the null hypothesis at \(5\)% level of significance. We conclude that the data does not show sufficient evidence that the mean rent expenses differ among students of different faculties.
Exercise 10.1 Statistically test if the rent expense differ among students of different genders.
10.2 Chi-square Test
In ANOVA, we can think of the different populations as categories of one categorical variable.
Example 10.5 In Example @ref(exm:#ex-other-rent-faculty-assump), Arts, Engineering, Environment, Health, Math and Science can be thought of as 6 categories of a variable about “faculty”.
The question whether the rent expense of students from all faculties are the same is equivalent to the question whether faculty affect the mean rent expense of students.
This is why in the R code of Example 10.1, we input the variable faculty as a possible explanatory variable of variable rent.
In ANOVA, because we assume normal distributions for each of the population, effectively we are working with a continuous response variable and one categorical explanatory variable.
But what if both our variables are categorical? In that case, we need to use the chi-square test to test whether the two variables are independent, i.e., if one variable affect the other variable.
Example 10.6 Suppose I want to know if the ratios of female, male, or students of other genders are the same among different faculty. This is equivalent to testing whether the distribution of variable gender differs among the different faculties of the variable faculty, which is also equivalent to testing whether faculty and gender are independent.
10.2.1 Assumptions
Each observation has to be of one category for each random variable.
There are at least five observations for each combination of the categories of the two variables.
Example 10.7 In Example 10.6, we when we conduct a Chi-square test, we have assumed that
each student is only categorized as either Female, Male or Others, and they cannot be both/all of Female, Male or Others. Similarly, each student belongs to only one faculty among Arts, Engineering, Environment, Health, Math or Science.
For each combination of gender and faculty, we collected data from at least five students. For example, we have data about at least five male students in Environment, etc.
10.2.2 Hypotheses
Suppose we have two categorical variables \(X\) and \(Y\). In a Chi-square test, we test the hypotheses
\(H_0\): \(X\) and \(Y\) are independent
\(H_1\): \(X\) and \(Y\) are dependent
Example 10.8 In Example 10.6, we want to test if gender and faculty are independent.
10.2.3 Analysis in R
We use the function chisq.test() in R to conduct a Chi-square test.
Example 10.9 For the question in Example 10.6, we want to test whether the variable faculty and the variable gender of the data set fakeRent.csv are independent. We use the following code
#a chi-square test of the gender and faculty variables
#of the data set rent we loaded from fakeRent.csv as in anova
chisq.test(rent$gender, rent$faculty)##
## Pearson's Chi-squared test
##
## data: rent$gender and rent$faculty
## X-squared = 78.322, df = 10, p-value = 1.07e-12Again, there are many information included in the output of this test, but we just need to focus on the \(p\)-value. The outputed \(p\)-value is \(1.07e-12\), which is a very small number, and is surely smaller than the usual significance level \(\alpha = 0.05\). Therefore, we reject the null hypothesis at \(5\%\) significance level and conclude that there is sufficient evidence in the data to support the claim that gender and faculty are dependent, or, faculty affects the distribution of gender.
Exercise 10.2 Test statistically if study level and gender are independent using the data set fakeRent.csv.
Notes:
In a hypothesis test, always decide your level of significance before you see the data. If you do not have a level of significance in your mind, you either
use the usual \(\alpha = 5\%\) level of significance
report the \(p\)-value only and depending on the value of \(p\)-value, conclude if the evidence is relatively strong or not (to support your null hypothesis).
Read more about the chi-square test here.
10.3 Levene’s Test
The Levene’s test is used to compare the variances of different populations. You can think of the Levene’s test as a version of ANOVA, but applied to the variances, instead of the means. The test can be useful in cases where
our main interest is the variance, not the mean. For example, we want to know whether a new machine can fill bottles more precisely than the old machine.
we want to check the equal variance assumption for our ANOVA procedure.
10.3.1 Hypotheses
The Levene’s test tests the hypotheses
\(H_0: \sigma_1 = \sigma_2 = ... = \sigma_m = \sigma\) where \(\sigma_i\) is the standard deviations of population \(i\), for \(1 \le i \le m\).
\(H_1:\) at least one of \(\sigma_i\) differs from the rest of the population standard deviations.
10.3.2 Analysis in R
The Levene’s test is basically just an ANOVA test for the absolute differences of the observations from the group means. To conduct the test in R, we use the function leveneTest() from the package car in R.
Example 10.10 We used ANOVA back in Example 10.4. Therefore, we would need to check for the assumption of equal variances among the rent expenses of students coming from the different faculties. We will do this using the Levene’s test.
First, you need to install the car package if you haven’t already
Now, you can run a Levene’s test in R as follows
## Loading required package: carData#run the levene test on the rent variable of data set rent
#the groups to be compared are different faculties
#the data about the faculties are encoded in variable faculty of data set rent
leveneTest(rent$rent, rent$faculty)## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 5 0.384 0.86
## 1339Again, we just need to focus on the \(p\)-value, which is 0.86 in this case. Since the \(p\)-value is greater than our usual level of significance \(\alpha = 0.05\), we do not reject the null hypothesis at \(5\%\) level of significance and we conclude that the data suggests the variances of the student’s rent expenses are the same among different faculty.
Exercise 10.3 Check the equality of variance assumption for the test in Exercise 9.1
10.4 QQ plot
With the Levene’s test, we have checked the equality of variance assumption for ANOVA. What about the assumption of normal distribution? We can use a QQ plot.
The QQ plot plots the sample quantiles of the data against the theoretical quantiles of the standard normal distribution. If
The points on the plot form a straight line (maybe with some slight departure at the two ends of the diagonal line), we can say that the distribution of the data is roughly normal.
Otherwise, the distribution of the data does not follow a normal distribution.
It is best to illustrate this using an example in R using the function qqnorm().
Example 10.11 Continue with Example 10.4, now let us check the normality assumption. In the ANOVA, we assumed that the rent expenses of students coming from each faculty follows a normal distribution.
To check if the rent expenses of students coming from Arts follows a normal distribution, we use the following code
#check whether the distribution of the rent variable
#for observations coming from Arts faculty,
#i.e., for observations where the value of variable faculty equals to "Arts"
qqnorm(rent$rent[rent$faculty == "Arts"])
#add a reference line to the qqnorm plot
#0.2 and 0.8 are the quantiles where the line is drawn
qqline(rent$rent[rent$faculty == "Arts"],
probs = c(0.2, 0.8))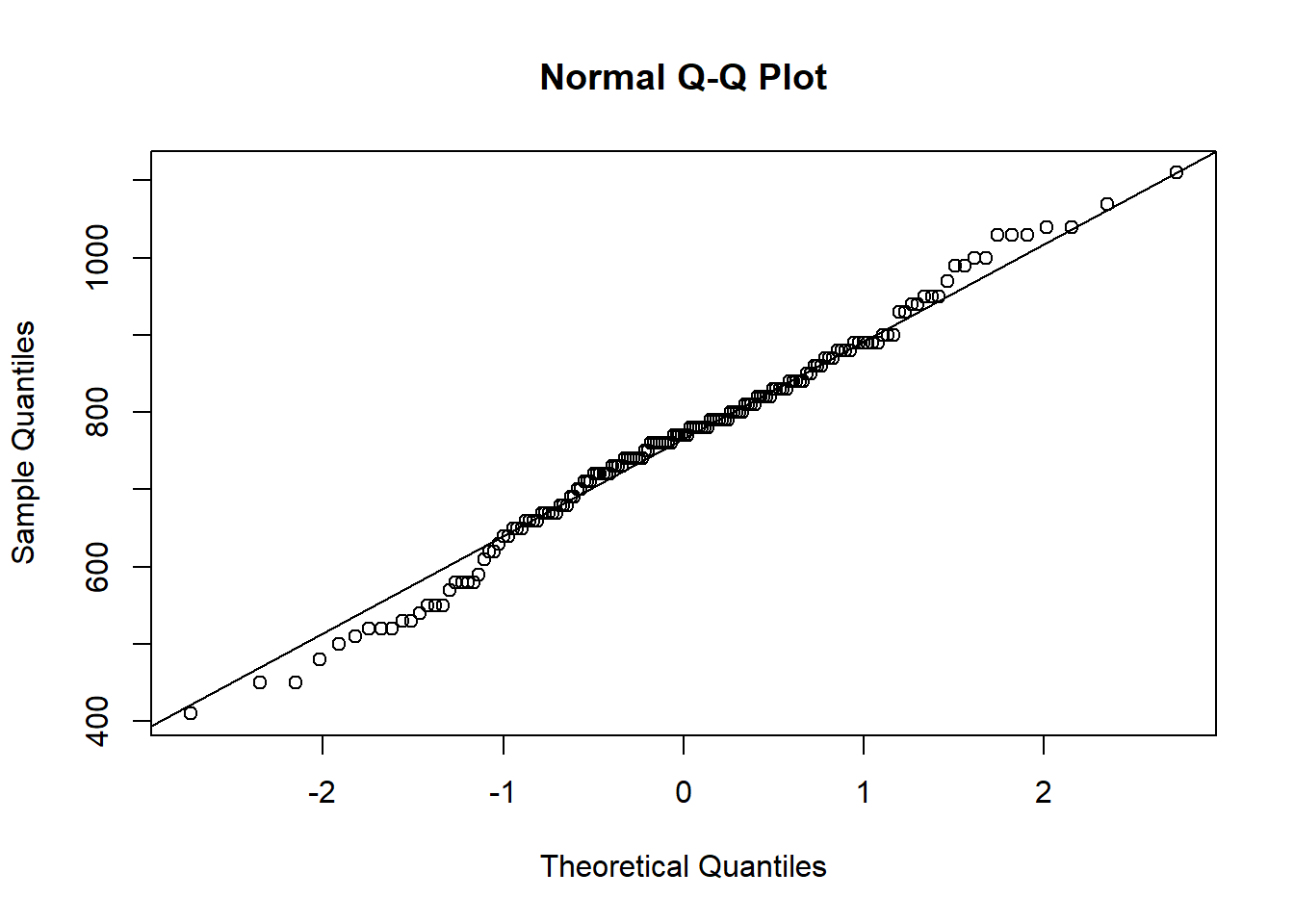
The points on the plot form a reasonably straight line, therefore, the normal assumption is quite reasonable for the rent expenses for Arts students.
Now, if we want to plot QQplots for students from all faculties, we use the following code
#create a grid of two rows and three columns for the plots
par(mfrow=c(2,3))
#arts faculty
qqnorm(rent$rent[rent$faculty == "Arts"],
main = "Arts students' rent")
qqline(rent$rent[rent$faculty == "Arts"],
probs = c(0.2, 0.8))
#engineering faculty
qqnorm(rent$rent[rent$faculty == "Engineering"],
main = "Engineering students' rent")
qqline(rent$rent[rent$faculty == "Engineering"],
probs = c(0.2, 0.8))
#environment faculty
qqnorm(rent$rent[rent$faculty == "Environment"],
main = "Environment students' rent")
qqline(rent$rent[rent$faculty == "Environment"],
probs = c(0.2, 0.8))
#health faculty
qqnorm(rent$rent[rent$faculty == "Health"],
main = "Health students' rent")
qqline(rent$rent[rent$faculty == "Health"],
probs = c(0.2, 0.8))
#math faculty
qqnorm(rent$rent[rent$faculty == "Math"],
main = "Math students' rent")
qqline(rent$rent[rent$faculty == "Math"],
probs = c(0.2, 0.8))
#science faculty
qqnorm(rent$rent[rent$faculty == "Science"],
main = "Science students' rent")
qqline(rent$rent[rent$faculty == "Science"],
probs = c(0.2, 0.8))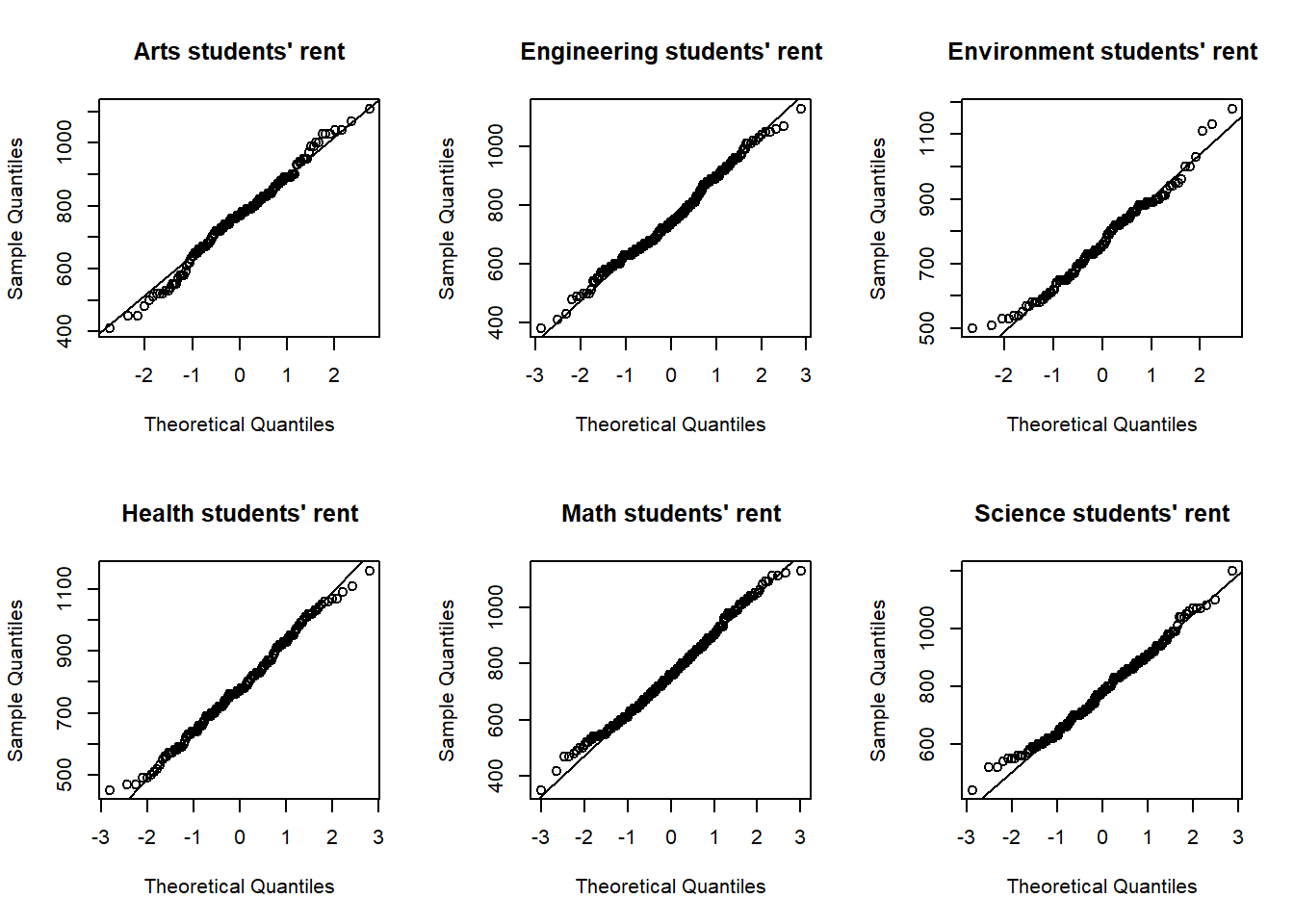
Based on the plots, we can see that our data seem to satisfy the normality (normal distributions) assumption.
Exercise 10.4 Check the normality assumption for the test in Exercise 9.1
Notes: There are statistical tests for normality as well. A popular test for normality is called the Shapiro-Wilk test. You can use function shapiro.test() to conduct the test in R.
10.5 Nonparametric Tests
To make statistical tests work, we have made some assumptions about our data.
For \(t\)-tests, we assume the two distributions are normally distributed. However, we learned that the test can still be used if
\(n < 15\), and the data is close to normal (symmetric, unimodal, no outliers)
\(n \ge 15\), except if the distribution is strongly skewed or if it has outliers
\(n \ge 40\): any distribution is fine.
For ANOVA, we assume that the distributions are normal and have equal variances. ANOVA can still be used
when normality assumption is slightly violated (the distribution is not heavily skewed, and there is no outliers)
when the largest variance is at most four times more than the smallest variance, as long as the sample sizes are the same (\(n_1 = n_2 = ... = n_m = n\))
What should we do if these conditions/assumptions are violated? For example, when the data is so expensive to collect that our sample size is too small? Or when the variances are so strongly different for ANOVA and the sample sizes are not the same?
In these cases, we come to hypothesis tests that require less/different assumptions. These alternative tests usually do not require an assumption about population parameters. For such a reason, they are called nonparametric tests.
10.6 Wilcoxon’s Rank Sum Test
The Wilcoxon’s rank sum test is a possible alternative for the two-sample \(t\)-tests we learn in Lesson 8.
10.6.1 Assumptions
The response variable is rankable (i.e., you can rank the observations of the response variable).
The two populations are of similar shapes and scales.
10.6.2 Hypotheses
Although we can think of the Wilcoxon’s rank sum test as a possible alternative to the \(t\)-test, the test tests a slightly different pair of hypotheses:
\(H_0:\) the median of the two distributions are the same
\(H_1:\) the median of the two distributions are not the same
10.6.3 Analysis in R
In R, we can run both unpaired independent and paired tests using the function wilcox.test() by choosing the correct option for the option paired inside the function.
Example 10.12 Suppose we want to know if the medians of rent expense are different among undergraduate and graduate students. We can think about running a two-sample \(t\)-test.
However, if the assumptions do not work, we can use a Wilcoxon’s rank sum test instead using the following code
#use a wilcoxon's rank sum test for rent expenses of
#undergraduate and graduate student
wilcox.test(rent$rent[rent$study == "Undergraduate"],
rent$rent[rent$study == "Graduate"],
alternative = "two.sided",
paired = FALSE)##
## Wilcoxon rank sum test with continuity correction
##
## data: rent$rent[rent$study == "Undergraduate"] and rent$rent[rent$study == "Graduate"]
## W = 263622, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 0We can see that the syntax of function wilcox.test() is quite similar to that of t.test().
Now, the \(p\)-value is \(2.2e-16\), which is almost 0. Therefore, it is smaller than our usual value \(\alpha = 0.05\). We reject the null hypothesis at \(5\%\) significance level and conclude that the medians of undergraduate and graduate’s rent expense are statistically significantly different.
Exercise 10.5 Use the Wilcoxon’s rank sum test to test if the rent price is higher when the room has a private washroom.
Notes: Suppose that the two populations you are testing are \(X\) and \(Y\). And further suppose that we are not willing to make the assumption that the populations of \(X\) and \(Y\) are of similar shapes and scales, then with the Wilcoxon’s rank sum test (the two-sided version), we are testing
\(H_0: \mathbb{P}(X > Y) = \mathbb{P}(X < Y)\), i.e., the probability of an observation from population \(X\) exceeding an observation from population \(Y\) is the same as the probability of an observation from \(Y\) exceeding an observation from \(X\);
\(H_1: \mathbb{P}(X > Y) \ne \mathbb{P}(X < Y)\).
10.7 Kruskal-Wallis test
This test is an ANOVA version of the Wilcoxon’s rank sum test, i.e., it is used to test more than two populations.
10.7.1 Assumptions
The response variable is rankable
The populations or all groups are similarly shaped and scaled, except for (possibly) any difference in medians
10.7.2 Hypotheses
\(H_0:\) the median of the distributions are the same
\(H_1:\) the median of the distributions are not the same
10.7.3 Analysis in R
In R, we use the function kruskal.test() to conduct a Kruskal-Wallis test.
Example 10.12 Although we can use an ANOVA as we did in Example 10.4, let’s apply the Kruskal-Wallis test to rent expenses of students of different faculties.
#kruskal-wallis test of the rent variable
#among the different categories of the variable faculty
#from the data set rent
kruskal.test(rent~faculty, data = rent)##
## Kruskal-Wallis rank sum test
##
## data: rent by faculty
## Kruskal-Wallis chi-squared = 7.6994, df = 5, p-value = 0.1736The \(p\)-value is \(0.1736\), which is greater than \(\alpha = 0.05\). Therefore, we do not reject the null hypothesis at \(5\%\) significance level and conclude that the data suggests the median rent expenses are the same among students of different faculties.
Exercise 10.6 Plot a side-by-side boxplot of the student’s rent among students of different genders. Use the Kruskal-Wallis test to test if the medians are the same. Look at the boxplot and see if the assumption of similarly shaped and scaled populations is reasonable.
10.8 Summary of the Tests
| Test | What to test | Function in R |
|---|---|---|
| ANOVA | Test equality of means of two or more populations | aov() |
| Chi-square test | Test if two categorical variables are independent | chisq.test() |
| Levene’s test | Test equality of variances of two or more populations | leveneTest() in package car |
| QQplot | Check normality assumption by plots | qqnorm() and qqline() |
| Shapiro-Wilk test | Test normality assumption | shapiro.test() |
| Wilcoxon’s rank sum test | Test equality of medians of two populations | wilcox.test() |
| Kruskal-Wallis test | Test equality of medians of two or more populations | kruskal.test() |
Notes: We have learned many tests in this lesson. The mathematical reasoning behind these tests are involved and skipped for the conciseness and introductory purpose of this book. To use the tests, we should focus on understanding the idea (which test is used for what), the assumptions, and the hypotheses for each the test. Moreover, we need to know how to run the tests in R and interpret the results. These tests will be very helpful to any statistical project you conduct in the future.